貯蓄行動と利子所得
利子所得税は、貯蓄に対する利子所得に課税される租税である。利子所得税の課税の効果を考えるには貯蓄を考慮しなければならず、貯蓄は将来消費するために充てられるから、現在の消費と将来の消費を考えなければならない。
そこで現在の消費と将来の消費を考える。いま、ある家計は現在のみ働いてWだけ所得を得たとする(ここでは労働時間が非弾力的でWは一定であるとする)。将来は引退して働かないため労働による所得はないものとする。このとき、この家計は現在消費と将来消費をどれだけにするかを決める。そこで、現在消費量をx1、将来消費量をx2とする。現在Wの所得を得て、それを現在消費にx1だけ充て、残りは貯蓄して将来消費に充てることとなる。貯蓄をsと表してこの関係を表すと、
W=x1+s (5)
となる。将来時点において、労働による所得はないがsだけの貯蓄がある。しかも、その貯蓄には利子率r(×100%)で利子所得が生じるとすると、将来時点では貯蓄と利子所得を合わせて(1+r)sだけの収入があり、これを将来消費に充てる。注A1 したがって、この関係を表すと、
(1+r)s=x2 (6)
となる。(5)式と(6)式を合わせると、この家計の生涯を通じた予算制約式は、
x2

また、この家計は現在消費と将来消費から効用を得るとする。家計の効用は現在、将来の消費量が多いほど高くなるとする。このとき、効用関数は一般的に
U=U(x1, x2)
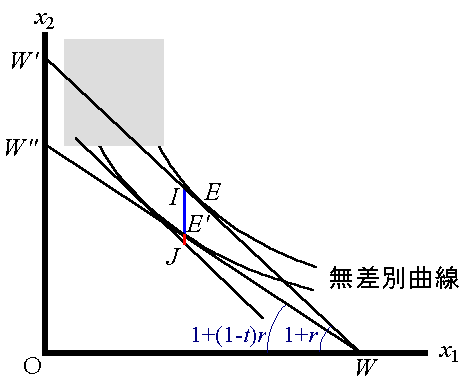
となる。ただし、現在消費、将来消費とも上級財であるとする。この効用関数から無差別曲線を導き出して図A4−1に示すと、点Eが効用最大化点となる。
利子所得税
次に、政府が利子所得税を課税することを考える。利子所得税率をt(×100%)とする。このとき、利子所得に対する課税額Tは、
T=trs
である。労働による所得には課税されない。したがって、現在消費についての(5)式は課税後も変わらない。しかし、利子所得がある(6)式は、課税後には次のようになる。
x2=(1+r)s−T={1+(1−t)r}s
この式と(5)式から、課税後の家計の生涯を通じた予算制約式は、次のようになる。
x2
利子所得税の超過負担
利子所得税は、代替効果が生じるから超過負担が生じ、効率性の観点から望ましくない。それでは、利子所得税によってどれだけ超過負担が生じるだろうか。これは、連載第4回第1節の労働所得税と同様に分析できる。
政府が利子所得税と同額の税収を一括固定税(人頭税)によって徴収できたとする。このとき、図A4−1において課税後の効用最大化点E'と同じ効用水準を得るように一括固定税を課税すれば、課税額がどれだけ変化するかを確認する。
利子所得税は課税せず、現在の所得に一括固定税をvだけ徴収すると、予算制約式は
x2
脚注
A1) 生涯で得た所得は全て消費し、遺産を残さないとする。
Copyright © 2001 Takero DOI All rights reserved.
元へ戻る